Eigenvalue localization for complex matrices
DOI:
https://doi.org/10.22199/S07160917.1992.0001.00003Keywords:
eigenvaluesAbstract
In this paper, we prove that all the eigenvalues ?i of a complex matrix A of order n lie in a disk with center at trA/n and radius
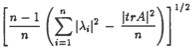
This radius can be bounded without knowing the eigenvalues of A.
References
[ 1] Eberlein, P.J.: On Measure of Non-normality for Matrices. American Mathematical Monthly, 72, pp 995-996, 1965.
[ 2] Rojo, O. and Soto, R .. New Conditions for the Additive Inverse Eigenvalue Problem for Matrices. Computers and Mathematics with Applications. To appear.
[ 3] Tarazaga, P.: Eigenvalue Estimate for Symmetric Matrices. Linear Algebra and Its Applications,135, pp 171-179, 1990.
[ 2] Rojo, O. and Soto, R .. New Conditions for the Additive Inverse Eigenvalue Problem for Matrices. Computers and Mathematics with Applications. To appear.
[ 3] Tarazaga, P.: Eigenvalue Estimate for Symmetric Matrices. Linear Algebra and Its Applications,135, pp 171-179, 1990.
Published
2018-04-02
How to Cite
[1]
Óscar L. Rojo Jeraldo, R. L. Soto Montero, H. Rojo J., and T.-. Y. Tam, “Eigenvalue localization for complex matrices”, Proyecciones (Antofagasta, On line), vol. 11, no. 1, pp. 11-19, Apr. 2018.
Issue
Section
Artículos
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.












