Chromatic coloring of distance graphs, III

Abstract

A graph G(Z, D) with vertex set Z is called an integer distance graph if its edge set is obtained by joining two elements of Z by an edge whenever their absolute difference is a member of D. When D = P or D ⊆ P where P is the set of all prime numbers then we call it a prime distance graph. After establishing the chromatic number of G(Z, P ) as four, Eggleton has classified the collection of graphs as belonging to class i if the chromatic number of G(Z, D) is i. The problem of characterizing the family of graphs belonging to class i when D is of any given size is open for the past few decades. As coloring a prime distance graph is equivalent to producing a prime distance labeling for vertices of G, we have succeeded in giving a prime distance labeling for certain class of all graphs considered here. We have proved that if D = {2, 3, 5, 7, 7^th prime, 10^th prime, 13^th prime, 16^th prime, (7 +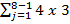^j)^th  prime, ..., (4 + 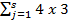^j)^th  prime for any s ∈ N}, then there exists a prime distance graph with distance set D in class 4 and if D = {2, 3, 5, 4^th prime, 6^th prime, 8^th prime, (4 + 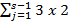^j)^th  prime, ..., (2 + 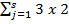^j)^th   prime for any s ∈ N} then there exists a prime distance graphs with distance set D in class 3. Further, we have also obtained some more interesting results that are either general or existential such as a) If D is a specific sequence of integers in arithmetic progression then there exist a prime distance graph with distance set D, b) If G is any prime distance graph in class i for 1 ≤ i ≤ 4 then G × K₂ is also a prime distance graph in the respective class i, c) A countable union of disjoint copies of prime distance graph is again a prime distance graph, d) The Middle/Total graph of a path on n vertices is a prime distance graph. In addition we also provide a new different proof for establishing a fact that all cycles are prime distance graph.