An Overview of Cubic Intuitionistic β-Subalgebras

Authors

  • Prakasam Muralikrishna Muthurangam Government Arts College (Autonomous),
  • A. Borumand Saeid Shahid Bahonar University of Kerman.
  • R. Vinodkumar Prathyusha Engineering College.
  • G. Palani Dr. Ambedkar Government Arts College.

DOI:

https://doi.org/10.22199/issn.0717-6279-4929

Keywords:

Cubic set, Cubic β−algebra, Cubic β−subalgebra, Cubic intuitionistic set, Cubic intuitionistic β−subalgebra

Abstract

The conditions  of β-algebra is enforced into the structure of cubic intuitionistic fuzzy settings. Furthermore, the concept of cubic intuitionistic  β-subalgebra  is expressed and its pertinent properties were explored. Also, discussed about the level set of cubic intuitionistic  β-subalgebras and  furnished some fascinating results on the cartesian  product of cubic intuitionistic  β-subalgebra.  Moreover, the notion of 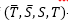mceclip0.png-normed cubic intuitionistic  β-subalgebras have been introduced and relevant results are studied.

Author Biographies

Prakasam Muralikrishna, Muthurangam Government Arts College (Autonomous),

Department of Mathematics.

A. Borumand Saeid, Shahid Bahonar University of Kerman.

Department of Pure Mathematics, Faculty of Mathematics and Computer,

R. Vinodkumar, Prathyusha Engineering College.

Department of Mathematics.

G. Palani, Dr. Ambedkar Government Arts College.

Department of Mathematics,

References

M. A. A. Ansari and M. Chandramouleeswaran, ”Fuzzy β−subalgebras of β−algebras”, International Journal of Mathematical Sciences and Engineering Applications, vol. 7, no. 5, pp. 239-249, 2013.

M. Akram, N. Yaqoob, and M. Gulistan, “Cubic Ku-Subalgebras”, International journal of pure and applied mathematics, vol. 89, no. 5, pp. 659–665, 2013.https://doi.org/10.12732/ijpam.v89i5.2

K. T. Atanassov, “Intuitionistic fuzzy sets”, Fuzzy sets and systems, vol. 20, no. 1, pp. 87–96, 1986. https://doi.org/10.1016/s0165-0114(86)80034-3

R. Biswas, “Rosenfelds fuzzy subgroups with interval-valued membership functions”, Fuzzy sets and systems, vol. 63, no. 1, pp. 87–90, 1994. https://doi.org/10.1016/0165-0114(94)90148-1

A. Borumand Saeid, P. Muralikrishna and P. Hemavathi, ”Bi-normed intuitionistic fuzzy β-ideals of β-algebras”, Journal of uncertain systems, vol. 13, no. 1, pp. 42-55, 2019. [On line]. Available: https://bit.ly/33dswIU

A. J. Dutta and B. C. Tripathy, “On the class of p-absolutely sumable sequence ℓi(p) of interval numbers”, Songklanakarin journal of science and technology, vol. 38, no. 2, pp. 143–146, 2016. [On line]. Available: https://bit.ly/3zyGVvl

P. Hemavathi, P. Muralikrishna, and K. Palanivel, ”A note on interval valued fuzzy β-subalgebras”, Global journal of pure and applied mathematics, vol. 11, no. 4, pp. 2553-2560, 2015.

P. Hemavathi, P. Muralikrishna, and K. Palanivel, ”On interval valued intuitionistic fuzzy β-subalgebras”, Afrika matematika, vol. 29, no. 1, pp. 249-262, 2018. https://doi.org/10.1007/s13370-017-0539-z

Y. B. Jun, C. S. Kim and K. O. Yang, ”Cubic sets”, Annals of fuzzy mathematics and informatics, vol. 4, no. 1, pp. 83-98, 2012. [On line]. Available: https://bit.ly/3JRxT0W

Y. B. Jun, C. S. Kim and M. S. Kang, ”Cubic subalgebras and ideals of BCK/BCI-algebras”, Far east journal of mathematical sciences, vol. 44, no. 2, pp. 239-250, 2010.

Y. B. Jun, “A novel extension of cubic sets and its applications in BCK/BCI-algebras”, Annals of fuzzy mathematics and informatics, vol. 14, no. 5, pp. 475–486, 2017. https://doi.org/10.30948/afmi.2017.14.5.475

Y. B. Jun, S.-Z. Song, and S. J. Kim, “Cubic interval-valued intuitionistic fuzzy sets and their application in BCK/BCI-algebras”, Axioms, vol. 7, no. 1, p. 1-17, 2018. https://doi.org/10.3390/axioms7010007

P. Muralikrishna, R. Vinodkumar, and G. Palani, “Some aspects on cubic fuzzy β-subalgebra of β-algebra”, Journal of physics: Conference series, vol. 1597, no. 1, pp. 012–018, 2020. https://doi.org/10.1088/1742-6596/1597/1/012018

N. Yaqoob, M. Khan, M. Akram and K. Asghar, “Interval valued intuitionistic (S,T)-fuzzy ideals of ternary semigroups”, Indian journal of science and technology, vol. 6, no. 11, pp. 5418-5428, 2013. https://doi.org/10.17485/ijst/2013/v6i11.7

J. Neggers and H. S. Kim, ”On β-algebras”, Mathematica slovaca, vol. 52, no. 5, pp. 517-530, 2002.

T. Senapati, Y. B. Jun, and K. P. Shum, “Cubic intuitionistic subalgebras and closed cubic intuitionistic ideals of B-algebras”, Journal of intelligent & fuzzy systems, vol. 36, no. 2, pp. 1563–1571, 2019. https://doi.org/10.3233/jifs-18518

B. C. Tripathy and A. J. Dutta, “Lacunary I-convergent sequences of fuzzy real numbers”, Proyecciones (Antofagasta), vol. 34, no. 3, pp. 205–218, 2015. https://doi.org/10.4067/s0716-09172015000300001

B. C. Tripathy and P. C. Das, ”On the class of fuzzy number sequences bvFP”, Songklanakarin journal of science and technology, vol. 41, no. 4, pp. 934-941, 2019. https://doi.org/10.14456/sjst-psu.2019.118

L. A. Zadeh, “Fuzzy sets”, Information and control, vol. 8, no. 3, pp. 338–353, 1965. https://doi.org/10.1016/s0019-9958(65)90241-x

Published

2022-01-28

How to Cite

[1]
P. Muralikrishna, A. . Borumand Saeid, R. . Vinodkumar, and G. Palani, “An Overview of Cubic Intuitionistic β-Subalgebras”, Proyecciones (Antofagasta, On line), vol. 41, no. 1, pp. 23-44, Jan. 2022.

Issue

Vol. 41 No. 1 (2022)

Section

Artículos

Copyright (c) 2022 Prakasam Muralikrishna, A. Borumand Saeid, R. Vinodkumar, G. Palani

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

  • No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.

Most read articles by the same author(s)