Existence and uniqueness of the generalized solution of a non-homogeneous hyperbolic differential equation modeling the vibrations of a dissipating elastic rod
DOI:
https://doi.org/10.22199/issn.0717-6279-4478Keywords:
dissipative evolution equation, existence and uniqueness of the generalized solutionAbstract
The purpose of this mathematical paper is to establish a qualitative research of the existence and uniqueness of the generalized solution to a non-homogeneous hyperbolic partial differential equation problema
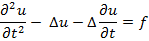
subject to the contour condition u = 0 over Σ, and with initial conditions u(x, 0) = u0(x) in Ω, ∂ut(x, 0) = u1(x) in Ω. In the development of the research, the deductive method of Faedo-Garleskin and Medeiro is used to demonstrate the existence of the generalized solution that consists in the construction of approximate solutions in a finite dimensional space, obtaining a succession of approximate solutions to the non-homogeneous hyperbolic problem, that is, by means of a priori estimations, these successions of approximate solutions are passed to limit in a suitable topology. Then the initial conditions are verified and the uniqueness of the generalized solution is proved.
References
R. A. Adams, Sobolev Space. Nueva York: Academic Press, 1975.
H. Brézis, Análisis Funcional. Madrid: Alianza Editorial, 1984.
F. E. Browder and Ton B. A, “Nonlinear Functional Equation in Banach Spaces and Elliptic Super Regularization”, Mathematische Zeitschrift, vol. 105, pp. 177-195, 1968. https://doi.org/10.1007/BF01109897
L. Evans, Partial Differential Equations. Graduate Studies in Mathematics, vol. 19. Providence, Rholde Island: American Mathematical Society,1998.
V. Kormonik and E. Zuazua, “A direct method for the boundary stabilization of the wave equation”, Journal de Mathématiques Pures et Appliquées, vol. 69, pp. 33-54, 1990.
J. Lions, Quelques Méthodes de Résolutions des Problemes aux limites non lineaires. Paris: Dunod, 1969.
L. A. Medeiros, Differential Equations of Evolution. Text Met. Mat. Rio de Janeiro, RJ, Brasil: IMUFRJ, 1990.
L. A Medeiros and M. Milla, Espacios de Sobolev. Rio de Janeiro, RJ, Brasil: Instituto de Matematica, UFRJ, 2000.
M. Nakao, “n the decay of solutions of some nonlinear dissipative wave equations”, Mathematische Zeitschrift, vol. 193, pp. 227-234, 1986.
M. Nakao, “n the decay of solutions of some nonlinear dissipative wave equations in higher dimensions”, Mathematische Zeitschrift, vol. 193, pp. 227-234, 1986. https://doi.org/10.1007/BF01174332
A. Ortiz, Basic aspects of equations in partial derivatives. Department of Mathematics of the National University of Trujillo, 1988.
W. Ray, Real Analysis. New Jersey: Prentice Hall, 1988.
J. M. Rivera, “Energy decay rates in linear thermo elasticity”, Funkcial EKVAC, vol. 35, pp. 9-30, 1992.
L. Schwartz, Mathematical Methods for the Physical Sciences. Scientific Selections. Madrid: Torres Quevedo, 1969. MED
E. Vera, An Introduction to Partial Differential Equations, Peruvian Mathematical Society Second Colloquium. Lima, 1984. VPO
Published
How to Cite
Issue
Section
Copyright (c) 2023 Jhony Alfonso Chávez Delgado, Augusto Becerra Castañeda, Luis César Méndez Avalos, Eduardo Rodríguez Delgado, Luis Asunción López Puycan

This work is licensed under a Creative Commons Attribution 4.0 International License.
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.












