Fractal mathematical over extended finite fields Fp[x]/(f(x))
DOI:
https://doi.org/10.22199/issn.0717-6279-4322Keywords:
Finite Galois extensions, Iterative multiplication over GF, Fractal design techniques, LFSR schemes, Self-similar circuits automorphismAbstract
In this paper, we have defined an algorithm for the construction of iterative operations, based on dimensional projections and correspondence between the properties of extended fields, with respect to modular reduction. For a field with product operations R(x) ⊗ D(x), over finite fields, GF[(pm)n−k]. With Gp[x]/(g(f(x)), whence the coefficient of the g(x) is replaced after a modular reduction operation, with characteristic p.
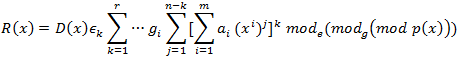
Thus, the reduced coefficients of the generating polynomial of contain embedded the modular reduction and thus simplify operations that contain basic finite fields. The algorithm describes the process of construction of the GF multiplier, it can start at any stage of LFSR; it is shift the sequence of operation, from this point on, thanks to the concurrent adaptation, to optimize the energy consumption of the GF iterative multiplier circuit, we can claim that this method is more efficient. From this, it was realized the mathematical formalization of the characteristics of the iterative operations on the extended finite fields has been developed, we are applying a algorithm several times over the coefficients in the smaller field and then in the extended field, concurrent form.
References
C. Carstensen, B. Fine, and G. Rosenberger, Abstract algebra: applications to Galois theory, algebraic geometry and cryptography. Berlin: de Gruyter, 2011.
T. W. Hungerford, “Fields and Galois theory”, in Algebra, New York, NY: Springer, 1974, pp. 230–310, doi: 10.1007/978-1-4612-6101-8_6
A. M. de Viola-Prioli, and J. E. Viola-Prioli, Teoría de grupos y teoría de Galois. Barcelona: Reverté, 2006.
E. Arohuata, "Una clasificación completa de los campos finitos", Tesis de Licenciatura en Ciencias Físico Matemáticas, Universidad Nacional del Altiplano - Puno, 2017. [On line]. Available: https://bit.ly/3y7mbth
C. E. Sandoval-Ruiz, “Modelo de estructuras reconfigurables con registro desplazamiento, para lenguaje descriptor de hardware VHDL”, Revista de la Facultad de Ingeniería, vol. 31, no. 3, pp. 63-72, 2016. [On line]. Available: https://bit.ly/2R5aEdA
L. A. Cortés Vega, “A general method for to decompose modular multiplicative inverse operators on Group of units”, Proyecciones (Antofagasta), vol. 37, no. 2, pp. 265-293, 2018. doi: 10.4067/S0716-09172018000200265
J. Avila, “Partial actions and quotient rings”, Proyecciones (Antofagasta), vol. 30, no. 2, pp. 201-212, 2011, doi: 10.4067/S0716-09172011000200006
C. E. Sandoval-Ruiz, “Codificador RS (n,k) basado en LFCS: caso de estudio RS (7,3)”, Revista Facultad de Ingeniería Universidad de Antioquia, no. 64, pp. 68-78, 2012. [On line]. Available: https://bit.ly/2SKbVqT
G. Reed and I. S. Solomon, “Polynomial codes on certain finite fields”, Journal of the Society for Industrial and Applied Mathematics, vol. 8, no. 2, pp. 300-304, 1960, doi: 10.1137/0108018
C. E. Sandoval-Ruiz, “Logical-mathematical model of encoder 2DRS for hardware description in VHDL”, Revista Ingeniería UC, vol. 24, no. 1, pp. 28-39, 2017. [On line]. Available: https://bit.ly/3uFgtN3
C. E. Sandoval Ruiz, “Multiplicador paralelo en campos finitos de Galois GF (2m) aplicado a códigos Reed Solomon con longitud ajustable sobre FPGA”, in Memorias VII Congreso Nacional y 1er Congreso Internacional de Investigación de la Universidad de Carabobo. La Investigación en el Siglo XXI: Oportunidades y Retos, vol. 2, Universidad de Carabobo and Consejo de Desarrollo Científico y Humanístico, Eds. Valencia: Universidad de Carabobo, 2010, pp. 1707–1711. [On line]. Available: https://bit.ly/3y2cE6X
C. E. Sandoval-Ruiz, “VHDL optimized model of a multiplier in finite fields”, Ingeniería y Universidad, vol. 21, no. 2, pp. 195-211, 2017. doi: 10.11144/Javeriana.iyu21-2.vhdl
G. C. Ahlquist, B. Nelson, and M. Rice, “Optimal finite field multipliers for FPGAs”, in Field programmable logic and applications, P. Lysaght, J. Irvine, and R. Hartenstein, Eds. Berlin: Springer, 1999, pp. 51–60, doi: 10.1007/978-3-540-48302-1_6
L. Cerda-Romero, and C. Martnez-Ranero, “The diophantine problem for addition and divisibility for subrings of rational functions over finite fields”, Proyecciones (Antofagasta), vol. 39, no. 3, pp. 721-735, 2020, doi: 10.22199/issn.0717-6279-2020-03-0045
C. E. Sandoval-Ruiz, “Modelo optimizado del codificador Reed-Solomon (255,k) en VHDL a través de un LFSR paralelizado”, Tesis de Doctorado, Universidad de Carabobo, Venezuela, 2013. [On line]. Available: https://bit.ly/3uFXfak
J. Großschädl and E. Savaş, “Instruction set extensions for fast arithmetic in finite fields GF (p) and GF (2m)”, in Cryptographic Hardware and Embedded Systems - CHES 2004, M. JoyeJean and J. Quisquater. Eds. Berlin: Springer, 2004, pp. 133-147, doi: 10.1007/978-3-540-28632-5_10
Z. Liu, H. Seo, J. Großschädl, and H. Kim, “Reverse product-scanning multiplication and squaring on 8-bit AVR processors”, in Information and communications security, L. C. K. Hui, S. H. Qing, E. Shi, and S. M. Yiu, Eds. Cham: Springer, 2014, pp. 158-175, doi: 10.1007/978-3-319-21966-0_12
C. E. Sandoval-Ruiz, “Operador matemático LFC(n,k) en campos finitos basado en concatenación fractal para GF (2m)Extendido”. Ciencia e Ingeniería (Mérida), vol. 41, no. 2, pp. 197-204, 2020. [On line]. Available: https://bit.ly/3hhTKmD
S. H. Weintraub, “Field theory and Galois theory” in Galois theory, 2nd Ed. New York, NY: Springer, 2009, pp. 7-44, doi: 10.1007/978-0-387-87575-0_2
C. E. Sandoval-Ruiz and A. Fedón-Rovira, “Efficient RS (255,k) encoder on reconfigurable systems”, Revista técnica de la Facultad de Ingeniería. Universidad del Zulia, vol. 37, no. 2, pp. 151-159, 2014. [On line]. Available: https://bit.ly/2QcBbVO
C. E. Sandoval Ruiz, “Power consumption optimization in Reed Solomon encoders on FPGA”, Latin American applied research (Online),vol. 44, no. 1, pp. 81-85, 2014, doi: 10.52292/j.laar.2014.422
C. E: Sandoval-Ruiz, “Métodos numéricos en diferencias finitas para la estimación de recursos de hardware FPGA en arquitecturas LFSR(n,k) fractales”. Ingeniería, investigación y tecnología (electrónica), vol. 20, no. 03, pp. 1-10, 2019. doi: 10.22201/fi.25940732e.2019.20n3.032
C. E. Sandoval-Ruiz, “Análisis de circuitos fractales y modelado a través de sistema de funciones iteradas para VHDL”, Ciencia e ingeniería (Mérida), vol. 38, no. 1, pp. 3-16, 2017. [On line]. Available: https://bit.ly/3w2jQOm
C. E. Sandoval-Ruiz, C., “LFSR-fractal ANN model applied in R-IEDs for smart energy”. IEEE Latin America transactions, vol. 18, no. 04, pp. 677-686, 2020, doi: 10.1109/tla.2020.9082210
C. E. Sandoval-Ruiz, “Arreglos fotovoltaicos inteligentes con modelo LFSR-reconfigurable”, Ingeniera, vol. 30, no. 2, pp. 32-61, 2020, doi: 10.15517/ri.v30i2.39484
C. E. Sandoval-Ruiz, “Arreglo inteligente de concentración solar FV para MPPT usando tecnología FPGA”, Revista Técnica de la Facultad de Ingeniería, vol. 43, no. 3, pp. 122-133, 2020, doi: 10.22209/rt.v43n3a02
C. E. Sandoval-Ruiz, “Tecnología R-IEDs para ERNC, teletrabajo y mitigación de impacto ambiental”, Industrial data, vol. 23, no. 2, pp. 151-167, 2020, doi: 10.15381/idata.v23i2.18633
C. E. Sandoval-Ruiz, “Laboratorio móvil para optimización de sistemas de energías renovables y aplicaciones ambientales”. Ciencia e ingeniería (Mérida), vol. 42, no. 2, 169-178, 2021. [On line]. Available: https://bit.ly/33OCihL
Published
How to Cite
Issue
Section
Copyright (c) 2021 Cecilia E. Sandoval-Ruiz

This work is licensed under a Creative Commons Attribution 4.0 International License.
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.












