On the multiplicative inverse eigenvalue problem
DOI:
https://doi.org/10.22199/S07160917.1988.0015.00001Keywords:
eigenvalue, operatorAbstract
An important inverse eigenvalue problem is the problem of finding a density q(x) such that the operator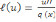 , with the appropriate boundary conditions, possesses o prescribed spectrum, that is, the inverse vibrating string problem.
, with the appropriate boundary conditions, possesses o prescribed spectrum, that is, the inverse vibrating string problem.
References
1. Biegler-Konig, F. W. Sufficient Conditions for the Solvability of Inverse Eigenvalue Problems. Linear Algebra and it Applications 40: 89-100, 1981.
2. De Oliveira, G. N. On the Multiplicative Inverse Eigenvalue Problem. Canadian Math. Bulletin 15: 189-193, 1972.
3. Dios da Silva, J.A. On the Multiplicative Inverse Eigenvalue Problem. Linear Algebra and its Applications 78: 133-145, 1986.
4. Downing, A. C. Jr. and Householder, A. S. Some Inverse Characteristic Value Problem. Journal Assoc. for Computing Machinery 3: 203-207, 1956.
5. Friedland, S. On Inverse Multiplicative Eigenvalue Problems for Matrices. Linear Algebra and its Applications 12: 127-137, 1975.
6. Hadeler, K. P. Multiplikative Inverse Eigenwertprobleme. Linear Algebra and i ts Appl. 2: 65-86, 1969.
7. Marcus, M. and Minc, H. A Survey of Matrix Theory and Matrix Inequalities. Allyn and Bacon, Boston, 1964.
8. Soto, R. On Matrix Inverse Eigenvalue Problems. Ph.D. Dissertation. New Mexico State University, U.S.A., 1987.
9. Wilkinson, J. H. The algebraic Eigenvalue Problem. Oxford University Press, London, 1965.
2. De Oliveira, G. N. On the Multiplicative Inverse Eigenvalue Problem. Canadian Math. Bulletin 15: 189-193, 1972.
3. Dios da Silva, J.A. On the Multiplicative Inverse Eigenvalue Problem. Linear Algebra and its Applications 78: 133-145, 1986.
4. Downing, A. C. Jr. and Householder, A. S. Some Inverse Characteristic Value Problem. Journal Assoc. for Computing Machinery 3: 203-207, 1956.
5. Friedland, S. On Inverse Multiplicative Eigenvalue Problems for Matrices. Linear Algebra and its Applications 12: 127-137, 1975.
6. Hadeler, K. P. Multiplikative Inverse Eigenwertprobleme. Linear Algebra and i ts Appl. 2: 65-86, 1969.
7. Marcus, M. and Minc, H. A Survey of Matrix Theory and Matrix Inequalities. Allyn and Bacon, Boston, 1964.
8. Soto, R. On Matrix Inverse Eigenvalue Problems. Ph.D. Dissertation. New Mexico State University, U.S.A., 1987.
9. Wilkinson, J. H. The algebraic Eigenvalue Problem. Oxford University Press, London, 1965.
Published
2018-03-28
How to Cite
[1]
R. L. Soto Montero, “On the multiplicative inverse eigenvalue problem”, Proyecciones (Antofagasta, On line), vol. 7, no. 15, pp. 1-20, Mar. 2018.
Issue
Section
Artículos
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.












