General solution and hyperstability results for a cubic radical functional equation related to quadratic mapping
DOI:
https://doi.org/10.22199/issn.0717-6279-2020-01-0007Keywords:
Stability, Hyperstability, Radical functional equationsAbstract
The aim of this paper is to introduce and solve the following radical cubic functional equation
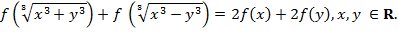
Also, we investigate some stability results for the considered equation in Banach spaces.
References
[1] L. Aiemsomboon and W. Sintunavarat, “On generalized hyperstability of a general linear equation”, Acta mathematica hungarica, vol. 149, no. 2, pp. 413-422, Aug. 2016, doi: 10.1007/s10474-016-0621-2.
[2] M. Almahalebi, A. Charifi and S. Kabbaj, “Hyperstability of a Cauchy functional equation”, Journal of nonlinear analysis and optimization: theory & applications, vol. 6, no. 2, pp. 127-137, 2015. [On line]. Available: https://bit.ly/2O7wqZf
[3] T. Aoki, “On the stability of the linear transformation in Banach spaces”, Journal of the mathematical society of Japan, vol. 2, no. 1-2, pp. 64-66, 1950, doi: 10.2969/jmsj/00210064.
[4] D. G. Bourgin, “Classes of transformations and bordering transformations”, Bulletin of the American mathematical society, vol. 57, no. 4, pp. 223-237, 1951, doi: 10.1090/S0002-9904-1951-09511-7.
[5] J. Brzdęk and J. Tabor, “A note on stability of additive mappings”, in Stability of mappings of Hyers-Ulam type, T. M. Rassias, Ed. Palm Harbor, FL: Hadronic Press, 1994, pp. 19–22.
[6] J. Brzdęk, J. Chudziak, and Z. Páles, “A fixed point approach to stability of functional equations”, Nonlinear analysis: theory, methods & applications, vol. 74, no. 17, pp. 6728-6732, Dec. 2011, doi: 10.1016/j.na.2011.06.052.
[7] J. Brzdęk, Hyperstability of the Cauchy equation on restricted domains, Acta mathematica hungarica, vol. 141, no. 1-2, pp. 58-67, Oct. 2013, doi: 10.1007/s10474-013-0302-3.
[8] J. Brzdęk, “Remark 3. 16th International Conference on Functional Equations and Inequalities, Będlewo, Poland, May 17-23, 2015”, Annales universitatis paedagogicae cracoviensis. Studia mathematica, vol. 14, no. 1, p. 196, Dec. 2015, doi: 10.1515/aupcsm-2015-0012.
[9] M. Eshaghi Gordji, H. Khodaei, A. Ebadian, and G. H. Kim, “Nearly radical quadratic functional equations in p-2-normed spaces”, Abstract and applied analysis, Art. ID. 896032, 2012, doi: 10.1155/2012/896032.
[10] D. H. Hyers, “On the stability of the linear functional equation”, Proceedings of the National Academy of Sciences of the United States of America, vol. 27, no. 4 pp. 222-224, Apr. 1941, doi: 10.1073/pnas.27.4.222.
[11] H. Khodaei, M. Eshaghi Gordji, S. S. Kim, and Y. J. Cho, “Approximation of radical functional equations related to quadratic and quartic mappings”, Journal of mathematical analysis and applications, vol. 395, no.1, pp. 284-297, Nov. 2012, doi: 10.1016/j.jmaa.2012.04.086.
[12] S. S. Kim, Y. J. Cho and M. Eshaghi Gordji, “On the generalized Hyers-Ulam-Rassias stability problem of radical functional equations”, Journal of inequalities and applications, Art. ID. 186, Aug. 2012, doi: 10.1186/1029-242X-2012-186.
[13] G. Maksa and Z. Pales, “Hyperstability of a class of linear functional equations”, Acta mathematica academiae paedagogicae nyiregyhaziensis, vol. 17, no. 2, pp. 107-112, 2001. [On line]. Available: https://bit.ly/2RzfnBt
[14] Th. M. Rassias, “On the stability of the linear mapping in Banach spaces”, Proceeding of the American mathematical society, vol. 72, no. 1, pp. 297-300, 1978, doi: 10.1090/S0002-9939-1978-0507327-1.
[15] Th. M. Rassias, “Problem 16, 2°. The Twenty-seventh International Symposium on Functional Equations, August 14–24, 1989, Bielsko-BiałKatowice—Kraków, Poland”, Aequationes mathematicae, vol. 39, no. 2-3, pp. 292-293, Apr. 1990, doi: 10.1007/BF01833155.
[16] Th. M. Rassias, “On a modified Hyers-Ulam sequence”, Journal of mathematical analysis and applications, vol. 158, no. 1, pp. 106-113, Jun. 1991, doi: 10.1016/0022-247X(91)90270-A.
[17] S. M. Ulam, Problems in modern mathematics. New York, NY: John Wiley & Sons, 1964.
[2] M. Almahalebi, A. Charifi and S. Kabbaj, “Hyperstability of a Cauchy functional equation”, Journal of nonlinear analysis and optimization: theory & applications, vol. 6, no. 2, pp. 127-137, 2015. [On line]. Available: https://bit.ly/2O7wqZf
[3] T. Aoki, “On the stability of the linear transformation in Banach spaces”, Journal of the mathematical society of Japan, vol. 2, no. 1-2, pp. 64-66, 1950, doi: 10.2969/jmsj/00210064.
[4] D. G. Bourgin, “Classes of transformations and bordering transformations”, Bulletin of the American mathematical society, vol. 57, no. 4, pp. 223-237, 1951, doi: 10.1090/S0002-9904-1951-09511-7.
[5] J. Brzdęk and J. Tabor, “A note on stability of additive mappings”, in Stability of mappings of Hyers-Ulam type, T. M. Rassias, Ed. Palm Harbor, FL: Hadronic Press, 1994, pp. 19–22.
[6] J. Brzdęk, J. Chudziak, and Z. Páles, “A fixed point approach to stability of functional equations”, Nonlinear analysis: theory, methods & applications, vol. 74, no. 17, pp. 6728-6732, Dec. 2011, doi: 10.1016/j.na.2011.06.052.
[7] J. Brzdęk, Hyperstability of the Cauchy equation on restricted domains, Acta mathematica hungarica, vol. 141, no. 1-2, pp. 58-67, Oct. 2013, doi: 10.1007/s10474-013-0302-3.
[8] J. Brzdęk, “Remark 3. 16th International Conference on Functional Equations and Inequalities, Będlewo, Poland, May 17-23, 2015”, Annales universitatis paedagogicae cracoviensis. Studia mathematica, vol. 14, no. 1, p. 196, Dec. 2015, doi: 10.1515/aupcsm-2015-0012.
[9] M. Eshaghi Gordji, H. Khodaei, A. Ebadian, and G. H. Kim, “Nearly radical quadratic functional equations in p-2-normed spaces”, Abstract and applied analysis, Art. ID. 896032, 2012, doi: 10.1155/2012/896032.
[10] D. H. Hyers, “On the stability of the linear functional equation”, Proceedings of the National Academy of Sciences of the United States of America, vol. 27, no. 4 pp. 222-224, Apr. 1941, doi: 10.1073/pnas.27.4.222.
[11] H. Khodaei, M. Eshaghi Gordji, S. S. Kim, and Y. J. Cho, “Approximation of radical functional equations related to quadratic and quartic mappings”, Journal of mathematical analysis and applications, vol. 395, no.1, pp. 284-297, Nov. 2012, doi: 10.1016/j.jmaa.2012.04.086.
[12] S. S. Kim, Y. J. Cho and M. Eshaghi Gordji, “On the generalized Hyers-Ulam-Rassias stability problem of radical functional equations”, Journal of inequalities and applications, Art. ID. 186, Aug. 2012, doi: 10.1186/1029-242X-2012-186.
[13] G. Maksa and Z. Pales, “Hyperstability of a class of linear functional equations”, Acta mathematica academiae paedagogicae nyiregyhaziensis, vol. 17, no. 2, pp. 107-112, 2001. [On line]. Available: https://bit.ly/2RzfnBt
[14] Th. M. Rassias, “On the stability of the linear mapping in Banach spaces”, Proceeding of the American mathematical society, vol. 72, no. 1, pp. 297-300, 1978, doi: 10.1090/S0002-9939-1978-0507327-1.
[15] Th. M. Rassias, “Problem 16, 2°. The Twenty-seventh International Symposium on Functional Equations, August 14–24, 1989, Bielsko-BiałKatowice—Kraków, Poland”, Aequationes mathematicae, vol. 39, no. 2-3, pp. 292-293, Apr. 1990, doi: 10.1007/BF01833155.
[16] Th. M. Rassias, “On a modified Hyers-Ulam sequence”, Journal of mathematical analysis and applications, vol. 158, no. 1, pp. 106-113, Jun. 1991, doi: 10.1016/0022-247X(91)90270-A.
[17] S. M. Ulam, Problems in modern mathematics. New York, NY: John Wiley & Sons, 1964.
Published
2020-02-04
How to Cite
[1]
R. El Ghali, M. Almahalebi, and S. Kabbaj, “General solution and hyperstability results for a cubic radical functional equation related to quadratic mapping”, Proyecciones (Antofagasta, On line), vol. 39, no. 1, pp. 107-122, Feb. 2020.
Issue
Section
Artículos
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.












