On some double sequence spaces of interval number.
Keywords:
Complete space, Interval number, Modulus function, Double sequence spaceAbstract
Esi and Yasemin defined the metric spaces 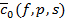 ,
, 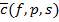 ,
, 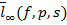 , and lp(f, p, s) of sequences of interval numbers by a modulus function. In this study, we consider a generalization for double sequences of these metric spaces by taking a ? function, satisfying the following conditions, instead of s parameter. For this aim, let ?(k, l) be a positive function for all k, l ? N such that
, and lp(f, p, s) of sequences of interval numbers by a modulus function. In this study, we consider a generalization for double sequences of these metric spaces by taking a ? function, satisfying the following conditions, instead of s parameter. For this aim, let ?(k, l) be a positive function for all k, l ? N such that
(i) 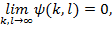
(ii) 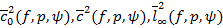
or
?(k, l) = 1.
Therefore, according to class of functions which satisfying the conditions (i) and (ii) we deal with the metric spaces 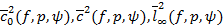 and
and 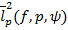 of double sequences of interval numbers defined by a modulus function.
of double sequences of interval numbers defined by a modulus function.
References
Chiao,K. P., Fundamental properties of interval vector max-norm, Tamsui Oxford Journal of Mathematics. 18, (2), pp. 219-233, (2002).
Dwyer, P. S., Linear Computation, Wiley, New York, 1951.
Dwyer, P. S., Error of matrix computation, simultaneous equations and eigenvalues, National Bureu of Standarts, Applied Mathematics Series. 29, pp. 49-58, (1953).
Esi, A., Strongly almost λ-convergence of interval numbers, Scientia Magna, 7 (2), pp. 117-122, (2011).
Esi, A., Lacunary sequence spaces of interval numbers, Thai Journal of Mathematics, 10 (2), pp. 445-451, (2012).
Esi, A., λ sequence spaces of interval numbers, Appl. Math. Inf. Sci, 8, (3), pp. 1099-1102, (2014).
Esi, A., A new class of interval numbers, Journal of QafQaz University, Mathematics and Computer Sciences, pp. 98-102, (2012).
Esi, A., Double lacunary sequence spaces of double sequence of interval numbers, Proyecciones Journal of Mathematics. 31, (1), pp. 297-306, (2012).
Esi, A. and Yasemin, S., Some spaces of sequences of interval numbers defined by a modulus function, Global Journal of Mathematical Analysis, 2, (1), pp. 11-16, (2014).
Esi, A., A new class of double interval numbers, Scientia Magna, 4(7), pp. 23-28, (2011).
Esi, A., Statistical and lacunary statistical convergence of interval numbers in topological groups, Acta Scientarium. Techno., 36 (3), pp. 491- 495, (2014).
Esi, A. and Hazarika, B., Some double sequence spaces of interval numbers defined by Orlicz function, Journal of the Egyptian Mathematical Society, 22, (3), pp. 424-427, (2014).
Esi, A and Esi, A., Asymptotically lacunary statistically equivalent sequences of interval numbers, Int. J. Math. Appl., 1 (1), pp. 43-48, (2013).
Esi, A. and Braha, N., On asymptotically λ-statistical equivalent sequences of interval numbers, Acta Scientarium. Techno., 35 (3), pp. 515-520, (2013).
Esi, A., Strongly λ-Summable Sequences of interval numbers, International Journal of Science, Environment and Technology, 5 (6), pp. 4643-4648, (2016).
Esi, A. and Catalbas, N., Some sequence spaces of interval numbers defined by Orlicz functions, Proceedings of the Jangjeon Mathematical Society, 20 (1), pp. 35-41, (2017).
Fischer, P. C., Automatic propagated and round-off error analysis, paper presented at the 13th National Meeting of the Association of Computing Machinary, June (1958).
Maddox, I. J., Spaces of strongly summable sequences, Quart. J. Math., Oxford Ser. 18, (2), pp. 345—355, (1967).
Markov, S., Quasilinear spaces and their relation to vector spaces, Electronic Journal on Mathematics of Computation, 2, (1), (2005).
Moore, R. E., Automatic Error Analysis in Digital Computation, LSMD-48421, Lockheed Missiles and Space Company, (1959).
Moore, R. E. and Yang, C. T., Theory of an Interval Algebra and Its Application to Numeric Analysis, RAAG Memories II, Gaukutsu Bunken Fukeyu-kai, Tokyo, (1958).
Moore, R. E. and Yang, C. T., Interval Analysis I, LMSD-285875, Lockheed Missiles and Space Company, (1962).
Pringsheim, A., Zur Theorie der zweifach unendlichen Zahlenfolgen, Math. Ann. 53, pp. 289—321, (1900).
Şengönül, M. and Eryılmaz, A., On the sequence spaces of interval numbers, Thai Journal of Mathematics. 8, (3), pp. 503—510, (2010)
Published
How to Cite
Issue
Section
-
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits.











